Inequality 6

July 2, 2014 by Hoàng Đức Hưng

Cho $a,b,c$ là ba số thực không âm và hai trong ba số không đồng thời bằng $0$ .
CMR: $\displaystyle{\sum \frac{1}{4a^2+b^2+c^2}\geq \frac{1}{2(a^2+b^2+c^2)}+\frac{1}{ab+bc+ca}} \qquad \triangle$ .
Lời Giải
Cách 1:
Ta nhân hai vế với $4(a^2+b^2+c^2)$ .
Ta có: $\displaystyle{\sum \frac{(4a^2+b^2+c^2)+3(b^2+c^2)}{4a^2+b^2+c^2}\leq 2+\frac{4(a^2+b^2+c^2)}{ab+bc+ca}}$
$\Leftrightarrow \displaystyle{\sum \frac{6a^2}{4a^2+b^2+c^2}+\frac{2(a^2+b^2+c^2)}{ab+bc+ca}\geq 5}$
$\Leftrightarrow \displaystyle{\sum \frac{6a^2}{4a^2+b^2+c^2}+\frac{2(a+b+c)^2}{ab+bc+ca}\geq 9}$
Mặt khác, áp dụng bất đẳng thức C-S:
Ta có: $\displaystyle{\sum \frac{6a^2}{4a^2+b^2+c^2}\geq \frac{(a+b+c)^2}{a^2+b^2+c^2}}$
Do đó, ta chỉ cần CM:
$\displaystyle{(a+b+c)^2(\frac{1}{a^2+b^2+c^2}+\frac{2}{ab+bc+ca})\geq 9}$
$\Leftrightarrow \displaystyle{(a+b+c)^2.\frac{9}{(a+b+c)^2}\geq 9(DPCM)}$ $\blacksquare$

Cách 2:
Không mất tính tổng quát, chuẩn hóa $a^2+b^2+c^2=3$
Ta có: $BDT\Leftrightarrow \displaystyle{\frac{1}{3}(\sum \frac{1}{a^2+1})\leq \frac{1}{6}+\frac{1}{ab+bc+ca}}$
$\Leftrightarrow \displaystyle{\sum (\frac{1}{3a^2+3}-\frac{1}{3})\leq \frac{-5}{6}+\frac{1}{ab+bc+ca}}$
$\Leftrightarrow \displaystyle{\sum \frac{-a^2}{3(a^2+1)}\leq \frac{-5}{6}+\frac{1}{ab+bc+ca}}$
$\Leftrightarrow \displaystyle{\sum \frac{a^2}{3(a^2+1)}\geq \frac{5(ab+bc+ca)-6}{6(ab+bc+ca)}}$
Áp dụng bất đẳng thức C-S
Ta có: $\displaystyle{\sum \frac{a^2}{3(a^2+1)}\geq \frac{(a+b+c)^2}{3(a^2+b^2+c^2+3)}=\frac{2(ab+bc+ca)+3}{18}}$
Đặt $ab+bc+ca=x$
Cần CM: $\displaystyle{\frac{2x+3}{18}\geq \frac{5x-6}{6x}\Leftrightarrow (x-3)^2\geq 0(TRUE)}$
Vậy BĐT được CM, dấu bằng xảy ra khi $a=b=c$ thỏa mãn ĐK ban đầu $\blacksquare$

Inequality 5

June 28, 2014 by Hoàng Đức Hưng

Cho $a,b,c$ dương thỏa mãn $abc=1$ .
CMR: $\displaystyle{\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\geq \frac{3}{2}(a+b+c-1)}(*)$ .
Lời giải
Từ giả thiết $abc=1$ , đặt $a=\frac{y}{x}$ ; $b=\frac{z}{y}$ , $c=\frac{x}{z}$ (với $x,y,z>0$ ).
Ta có: $(*) \Leftrightarrow \displaystyle{\frac{y^2}{zx}+\frac{z^2}{xy}+\frac{x^2}{yz}\geq \frac{3}{2}\left ( \frac{y}{x}+\frac{z}{y}+\frac{x}{z}-1 \right )}$
$\Leftrightarrow \displaystyle{\frac{2(x^3+y^3+z^3)+3xyz}{xyz}\geq \frac{3(y^2z+z^2x+x^2y)}{xyz}}$
$\Leftrightarrow 2(x^3+y^3+z^3)+3xyz\geq 3(y^2z+z^2x+x^2y)$ $(**)$
Ta có các bất đẳng thức phụ sau:
+, Schur: $x^3+y^3+z^3+3xyz\geq xy(x+y)+yz(y+z)+zx(z+x)$ (1)
+, $x^3+y^3+z^3+x^2z+y^2x+z^2y\geq 2(x^2y+y^2z+z^2x)$ (2)
$\Leftrightarrow x(x-y)^2+y(y-z)^2+z(z-x)^2\geq 0(TRUE)$
Cộng vế theo vế hai bất đẳng thức (1) và (2) $\Rightarrow (**)TRUE\Rightarrow (*)TRUE$
Dấu bằng xảy ra $\Leftrightarrow x=y=z\Leftrightarrow a=b=c=1$ .
Vậy bất đẳng thức được chứng minh.

Chuỗi bất đẳng thức xây dựng từ các đẳng thức đã biết

June 24, 2014 by Hoàng Đức Hưng

Bất đẳng thức luôn là một trong những vấn đề toán học hấp dẫn nhất hiện nay, đặc biệt là các bất đẳng thức $3$ biến. Nó luôn có một vẻ đẹp rất “đáng yêu”, từ đó có rất nhiều học sinh, sinh viên đến các giáo sư tiến sĩ nghiên cứu bất đẳng thức. Trong đó, không thể thiếu được sự sáng tạo. Và bằng phương pháp sử dụng đẳng thức đã biết, anh Đào Hải Long (HCV IMO) đã có một chuỗi bất đẳng thức khá thú vị.

VD1: CMR với mọi $x,y,z$ là số thực phân biệt thì:
$\displaystyle{\frac{x^2}{(y-z)^2}+\frac{y^2}{(z-x)^2}+\frac{z^2}{(x-y)^2}\geq 2}$
Lời giải
Nhận xét: BĐT trên nhìn khá kì quặc vì lại có hiệu bình phương ở dưới mẫu. Lời giải như sau:
Giả sử $\displaystyle{x=\frac{a}{b-c},y=\frac{b}{c-a},z=\frac{c}{a-b}}$ , khi đó ta có:
$(1+x)(1+y)(1+z)=-(1-x)(1-y)(1-z)\Rightarrow xy+yz+zx=-1$
Do đó hiển nhiên $x^2+y^2+z^2\geq -2(xy+yz+zx)$ $\Leftrightarrow x^2+y^2+z^2\geq 2$
Vậy BĐT được chứng minh.

VD2: CMR với mọi $a,b,c$ thực phân biệt thì
$\displaystyle{\frac{(a+b)^2}{(a-b)^2}+\frac{(b+c)^2}{(b-c)^2}+\frac{(c+a)^2}{(c-a)^2}}$
Lời giải
Bất đẳng thức này CM giống hệt như trên, chú ý rằng:
$\displaystyle{\frac{a+b}{a-b}.\frac{b+c}{b-c}+\frac{b+c}{b-c}.\frac{c+a}{c-a}+\frac{c+a}{c-a}.\frac{a+b}{a-b}=-1}$
Đẳng thức xảy ra khi $(a+b)(b+c)(c+a)=8abc$ , chẳng hạn $c=0,a=-b$ .

Bớt đi $1$ vào mỗi hạng tử vế trái ta được BĐT mới
VD3: CMR với mọi $a,b,c$ thực phân biệt thì
$\displaystyle{\frac{ab}{(a-b)^2}+\frac{bc}{(b-c)^2}+\frac{ca}{(c-a)^2}\geq \frac{-1}{4}}$

Thêm vào $1$ ở mỗi hạng tử vế trái, ta được
VD4: CMR với mọi $a,b,c$ thưc phân biệt thì
$\displaystyle{\frac{a^2+b^2}{(a-b)^2}+\frac{b^2+c^2}{(b-c)^2}+\frac{c^2+a^2}{(c-a)^2}\geq \frac{5}{4}}$

Kết hợp với BĐT ở VD1, ta được
VD5: CMR với mọi $a,b,c$ thực phân biệt thì
$\displaystyle{\frac{1}{(a-b)^2}+\frac{1}{(b-c)^2}+\frac{1}{(c-a)^2}\geq \frac{9}{2(a^2+b^2+c^2)}}$

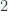Cộng $2$ kết quả ở VD3 và VD4 ta suy ra
VD6: CMR với mọi $a,b,c$ thực phân biệt thì
$\displaystyle{\frac{a^2+ab+b^2}{(a-b)^2}+\frac{b^2+bc+c^2}{(b-c)^2}+\frac{c^2+ca+a^2}{(c-a)^2}\geq \frac{9}{4}}$

Do đó, ta có kết quả đẹp mắt hơn nhưng tơng đương là
VD7: CMR với mọi $a,b,c$ thực phân biệt thì
$\displaystyle{\frac{a^3-b^3}{(a-b)^3}+\frac{b^3-c^3}{(b-c)^3}+\frac{c^3-a^3}{(c-a)^3}\geq \frac{9}{4}}$

Tóm lại, ta đã thấy rằng : Việc sử dụng liên tiếp các hằng đẳng thức và thêm bớt các biểu thức một cách hợp lí đã giúp chúng ta tạo ra những bất đẳng thức mới khá đẹp mắt. Chúng đứng thành một nhóm trong hệ thống xây dựng chung và nếu thiếu đi khâu trung gian thì sẽ rất khó để nghĩ ra được một lời giải tương tự. Vì thế, ta càn phải xem xét vấn đề theo cách khác.

Inequality 2

June 1, 2014 by Hoàng Đức Hưng

Cho $a,b,c>0$ thỏa $a+b+c=1$ .
CMR: $\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}$ $\geq 3(a^2+b^2+c^2)$ .
Lời giải
Áp dụng BĐT Cauchy – Schwarz:
Ta có: $latex \frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{a}= \frac{a^4}{a^{2}b}+\frac{b^4}{b^{2}c}+\frac{c^4}{c^{2}a}\geq \frac{(a^{2}+b^{2}+c^{2})^{2}}{a^{2}b+b^{2}c+c^{2}a}$
Áp dụng BĐT AM-GM:
Ta có: $a^2b=a\sqrt{a}.b\sqrt{a}\leq \frac{a^3+b^2a}{2}$ (1)
$b^2c=b\sqrt{b}.c\sqrt{b}\leq \frac{b^3+c^2b}{2}$ (2)
$c^2a=c\sqrt{c}.a\sqrt{c}\leq \frac{c^3+a^2c}{2}$ (3)
Cộng vế với vế (1),(2),(3)
Ta có: $a^2b+b^2c+c^2a\leq \frac{a^3+b^3+c^3+ab^2+bc^2+ca^2}{2}$
$=\frac{a^2(a+c)+b^2(b+a)+c^2(c+b)}{2}$
$=\frac{a^2(1-b)+b^2(1-c)+c^2(1-a)}{2}$
$\Leftrightarrow a^2b+b^2c+c^2a\leq \frac{a^2+b^2+c^2}{3}$
$\Rightarrow VT\geq \frac{3(a^2+b^2+c^2)^2}{a^2+b^2+c^2}=3(a^2+b^2+c^2)$
Dấu bằng xảy ra $\Rightarrow VT\geq \frac{3(a^2+b^2+c^2)^2}{a^2+b^2+c^2}=3(a^2+b^2+c^2)$
Vậy BĐT ban đầu được CM.

Inequality 1

May 28, 2014 by Hoàng Đức Hưng

Cho $a,b,c>0$ thỏa mãn $a+b+c=2$ .
Chứng minh rằng: $\sqrt{\frac{a+b}{2}-ab}+\sqrt{\frac{b+c}{2}-bc}+\sqrt{\frac{c+a}{2}-ca}\geq \sqrt{2}$ $(*)$
Lời Giải
Bất đẳng thức cần chứng minh $\Leftrightarrow \sqrt{a+b-2ab}+\sqrt{b+c-2bc}+\sqrt{c+a-2ca}\geq 2$
Vì vai trò $a,b,c$ như nhau nên giả sử $a\geq b\geq c$ , mà $a+b+c=2$ $\Rightarrow c\leq \frac{2}{3}$
Áp dụng BĐT AM-GM, ta có:
$\sqrt{a+b-2ab}\geq \sqrt{2-c-\frac{(a+b)^2}{2}}=\sqrt{2-c-\frac{(2-c)^2}{2}}=\sqrt{c-\frac{c^2}{2}}$
Mặt khác, ta có:
$\sqrt{b+c-2bc}=\sqrt{2-a-2(2-a-c)c}=\sqrt{2-a-4c+2ac+2c^2}=\sqrt{2(c-1)^2+a(2c-1)}\geq \sqrt{2(c-1)^2+c(2c-1)}=\sqrt{4c^2-5c+2}$
Tương tự: $\sqrt{c+a-2ca}\geq \sqrt{4c^2-5c+2}$
Đặt $A=\sqrt{b+c-2bc}+\sqrt{c+a-2ca}$
Ta có: $A^2=c+a-2ca+b+c-2bc+2\sqrt{(b+c-2bc)(c+a-2ca)}\geq c+a-2ca+2-a-4c+2ac+2c^2+2(4c^2-5c+2)\geq 10c^2-13c+6\Rightarrow A=\sqrt{10c^2-13c+6}$
Cần chứng minh: $\sqrt{10c^2-13c+6}+\sqrt{c-\frac{c^2}{2}}\geq 2$
Nhưng BĐT trên luôn đúng sau khi biến đổi tương đương.
Vậy BĐT $(*)$ được chứng minh, dấu đẳng thức khi $a=b=c=\frac{2}{3}$